
달시 바이스바하 (Darcy-Weisbach) 방정식에 대한 이론 정리
달시 바이스바하 (Darcy-Weisbach) 방정식은 유체가 관을 따라 흐를 때, 그 흐름 속에서 발생하는 마찰 손실을 계산하는 데 사용되는 매우 중요한 방정식입니다. 이 방정식은 다양한 관로 시스템의 설계와 분석에 필수적인 도구입니다.
1. 달시 바이스바하 (Darcy-Weisbach) 방정식이란?
관을 통해 유체(예: 물, 기름 등)가 흐를 때, 유체와 관의 표면 사이에서 마찰이 발생합니다. 이 마찰로 인해 압력 손실이나 에너지 손실이 생깁니다. 달시 바이스바하 (Darcy-Weisbach) 방정식은 이 손실을 계산하는 공식입니다.
이 방정식은 다음과 같은 형태로 주어집니다:
![]()
여기서,
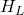 : 마찰 손실 수두 또는 압력 손실 (단위: m)
: 마찰 손실 수두 또는 압력 손실 (단위: m)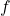 : 마찰 계수, 관의 표면 거칠기와 유체 흐름의 성격에 따라 달라지는 무차원 값
: 마찰 계수, 관의 표면 거칠기와 유체 흐름의 성격에 따라 달라지는 무차원 값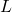 : 관의 길이 (단위: m)
: 관의 길이 (단위: m) : 관의 직경 (단위: m)
: 관의 직경 (단위: m)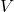 : 유속 (단위: m/s)
: 유속 (단위: m/s)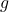 : 중력 가속도 (9.81 m/s²)
: 중력 가속도 (9.81 m/s²)
2. Darcy-Weisbach 방정식의 의미
이 방정식은 관의 길이, 직경, 유속, 그리고 마찰 계수가 마찰 손실 수두에 어떻게 영향을 미치는지 설명합니다.
- 마찰 계수(f): 유체가 흐를 때 관의 표면 거칠기와 유체 흐름의 성질에 따라 달라집니다. Reynolds 수를 계산한 후, 층류 또는 난류 상태에 따라 f 값을 결정합니다. 관이 매끄럽거나 유속이 느리면 마찰 계수가 작아지며, 거칠거나 유속이 빠르면 커집니다.
- 유속(V): 유체가 빠르게 흐를수록 마찰 손실이 커집니다. 방정식에서
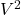 에 비례하므로 유속이 두 배로 증가하면 마찰 손실은 네 배로 커집니다.
에 비례하므로 유속이 두 배로 증가하면 마찰 손실은 네 배로 커집니다. - 관의 직경(D): 관의 직경이 클수록 마찰 손실이 줄어듭니다. 관이 넓으면 유체가 흘러가는 면적이 더 커지므로, 관이 좁을 때보다 마찰이 덜 발생합니다.
- 관의 길이(L): 관의 길이가 길수록 마찰 손실도 커집니다. 길이가 두 배로 길어지면 마찰 손실도 두 배로 증가합니다.
3. 마찰 계수(f) 구하는 법
마찰 계수 ![]() 는 Reynolds 수와 관의 거칠기에 따라 달라집니다. Reynolds 수는 유체가 층류 또는 난류로 흐르는지 판단하는 무차원 수입니다. Reynolds 수가 낮으면 층류, 높으면 난류입니다.
는 Reynolds 수와 관의 거칠기에 따라 달라집니다. Reynolds 수는 유체가 층류 또는 난류로 흐르는지 판단하는 무차원 수입니다. Reynolds 수가 낮으면 층류, 높으면 난류입니다.
- 층류(Re < 2000): 마찰 계수
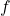 는 다음 공식으로 구할 수 있습니다:
는 다음 공식으로 구할 수 있습니다:
![Rendered by QuickLaTeX.com \[ f = \frac{64}{Re} \]](https://studywith.my/wp-content/ql-cache/quicklatex.com-81a9c537fbcb20f681372752b7843798_l3.png)
- 난류(Re > 4000): 난류에서는
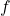 를 구하는 식이 복잡해지며, Colebrook-White 방정식 등을 사용해야 할 수 있습니다.
를 구하는 식이 복잡해지며, Colebrook-White 방정식 등을 사용해야 할 수 있습니다.
4. Darcy-Weisbach 방정식이 쓰이는 곳
Darcy-Weisbach 방정식은 다양한 실제 상황에서 사용됩니다. 예를 들어:
- 수도관 설계 시 물의 압력 손실을 계산하여 적절한 펌프 크기를 선택할 때
- 산업용 파이프 시스템에서 유체 흐름을 최적화하고 에너지 손실을 줄이기 위해
- 에어컨 배관 설계 시 공기 흐름의 저항을 계산할 때
5. Darcy-Weisbach 방정식과 관련된 요소들
- Reynolds 수: 유체 흐름이 층류인지 난류인지를 결정하는 중요한 수치로, 유체의 속도, 밀도, 점성, 관의 직경 등을 기반으로 계산됩니다.
- 마찰 손실: 유체가 관을 따라 흐르면서 발생하는 에너지 손실을 의미합니다.
- 관의 거칠기: 관의 표면이 매끄러운지, 거친지에 따라 마찰 계수가 달라집니다.
달시 바이스바하 예시 문제
길이가 100 m, 직경이 0.1 m인 관을 통해 유속 2 m/s로 물이 흐르고 있습니다. 마찰 계수 f = 0.03일 때, 마찰 손실 수두를 계산하세요.
해결 과정:
- 주어진 값을 식에 대입합니다:
![Rendered by QuickLaTeX.com \[ H_L = 0.03 \times \frac{100}{0.1} \times \frac{2^2}{2 \times 9.81} \]](https://studywith.my/wp-content/ql-cache/quicklatex.com-57312ff9a68fe230e3ffde82a15b3b81_l3.png)
- 계산하면:
![Rendered by QuickLaTeX.com \[ H_L = 0.03 \times 1000 \times \frac{4}{19.62} = 0.03 \times 1000 \times 0.204 = 6.12 \, \text{m} \]](https://studywith.my/wp-content/ql-cache/quicklatex.com-e51268c1a71564e251f3898246db5a2e_l3.png)
따라서 마찰 손실 수두 ![]() 는 6.12 m입니다.
는 6.12 m입니다.
결론
Darcy-Weisbach 방정식은 유체가 관을 따라 흐를 때 발생하는 마찰 손실을 계산하는 데 매우 유용한 도구입니다. 이를 통해 관의 크기, 유체 흐름 속도, 그리고 마찰 손실을 최적화하여 효율적인 시스템 설계가 가능합니다.
달시 바이스바하 연습문제
문제 1:
길이가 100 m이고 직경이 0.2 m인 관을 통해 물이 흐르고 있습니다. 유량은 0.05 m³/s이며, 마찰 계수 f = 0.02입니다. 중력 가속도 g = 9.81 m/s²로 가정할 때, 이 관을 통해 흐르는 물의 마찰 손실 수두(HL)는 얼마인가?
문제 2:
길이가 150 m, 직경이 0.1 m인 관을 통해 물이 유속 3 m/s로 흐르고 있습니다. 이때, Darcy-Weisbach 방정식을 이용하여 마찰 손실 수두를 구하세요. 마찰 계수 f = 0.03이며, 중력 가속도 g = 9.81 m/s²로 가정합니다.
문제 3:
직경이 0.15 m, 길이가 200 m인 관을 통해 유량이 0.06 m³/s인 물이 흐르고 있습니다. Darcy-Weisbach 방정식을 이용해 마찰 손실 수두를 계산하고, 마찰 계수가 0.025일 때 마찰 손실 수두는 얼마인가? 중력 가속도 g = 9.81 m/s²를 사용하세요.
문제 4:
관의 길이가 50 m, 직경이 0.05 m인 관을 통해 유속 4 m/s로 물이 흐르고 있습니다. 마찰 계수 f = 0.04일 때 Darcy-Weisbach 방정식을 이용해 마찰 손실 수두를 구하시오. 중력 가속도는 g = 9.81 m/s²로 가정합니다.
문제 5:
길이가 80 m이고, 직경이 0.3 m인 관을 통해 유량이 0.2 m³/s인 물이 흐르고 있습니다. 마찰 계수 f = 0.02이며, 중력 가속도 g = 9.81 m/s²로 가정할 때 Darcy-Weisbach 방정식을 이용해 마찰 손실 수두를 구하시오.
추가 연습문제 입니다.
문제 1
내경이 40cm, 길이가 500m인 배관에 유체가 유속 0.6m/s로 흐르고 있다. 마찰손실계수가 f = 0.04일 때, 배관에서 발생하는 마찰손실 수두와 상당구배를 계산하시오. (중력가속도 g = 9.8 m/s²)
문제 2
내경이 25cm, 길이가 800m인 배관에 유체가 유속 0.9m/s로 흐르고 있다. 마찰손실계수가 f = 0.05일 때, 배관에서 발생하는 마찰손실 수두와 상당구배를 계산하시오. (중력가속도 g = 9.8 m/s²)
문제 3
내경이 30cm, 길이가 600m인 배관에 유체가 유속 0.5m/s로 흐르고 있다. 마찰손실계수가 f = 0.03일 때, 배관에서 발생하는 마찰손실 수두와 상당구배를 계산하시오. (중력가속도 g = 9.8 m/s²)
문제 4
내경이 35cm, 길이가 1,200m인 배관에 유체가 유속 1.0m/s로 흐르고 있다. 마찰손실계수가 f = 0.02일 때, 배관에서 발생하는 마찰손실 수두와 상당구배를 계산하시오. (중력가속도 g = 9.8 m/s²)
문제 5
내경이 45cm, 길이가 700m인 배관에 유체가 유속 1.2m/s로 흐르고 있다. 마찰손실계수가 f = 0.06일 때, 배관에서 발생하는 마찰손실 수두와 상당구배를 계산하시오. (중력가속도 g = 9.8 m/s²)
문제 6
내경이 60cm, 길이가 900m인 배관에 유체가 유속 1.1m/s로 흐르고 있다. 마찰손실계수가 f = 0.045일 때, 배관에서 발생하는 마찰손실 수두와 상당구배를 계산하시오. (중력가속도 g = 9.8 m/s²)
